跳转到主要内容

C13

领读人：雪珊

录音转文字：📎5-2-集异璧第十三章共读.docx
录屏链接: https://pan.baidu.com/s/1BNap-1xAVzrYffrYiBZPxw?pwd=l26k 提取码: l26k

计算机编程 101

都包括啥？

  • 循环
  • 条件判断（IF）
  • 函数调用
  • 函数可以输出计算结果，也可以输出 YES 或 NO

—— 绿色块都是读者弹幕 ——

我觉得他用的编程语言的书写方式太啰嗦啦～容易看晕～就像是一句话非要把主谓宾定状补都说出来。如果某个成分没有，比如只讲“姑娘”不加定语，就必须要说成是「无定语姑娘」。

还是爱Python～～

用 Python 写 2^3^n 的计算函数～
def TWO_TO_THE_THREE_TO_THE (N):
	cell0 = 1
	i = 0
	while i < N:
		cell0 = 3 * cell0
		i = i + 1
		
	cell1 = 1
	i = 0
	while i < cell0:
		cell1 = 2 * cell1
		i = i + 1
	return cell1

玩了个小花招

  • 没有定义所有的代数运算（加减乘除、乘方开方……），而是取了个能生成它们的最小集合：
    • 自然数加法
    • 自然数乘法
    • 比较两个数是否相等
    • 比较两个数谁大谁小

不仅如此，所有的运算还都只限制在自然数里！不处理小数、负数……因为我们只用这个程序来计算数论里关于自然数的问题。好吧算你懒～

当然，计算机算自然数更自然一些……在它们还没有那么智能的年代，小数和负数怎么用二进制表示，计算的精度够不够，是个问题。不考虑的话，不小心就差大了。

所以，我怀疑还是侯世达懒。不，是学计算机学出的极简懒学后遗症！能限制的条件都要拿来作为限制条件！少用几条内存和CPU！

学数学，我们就从来不考虑这些。反正连数字都不用……草稿纸又不要钱



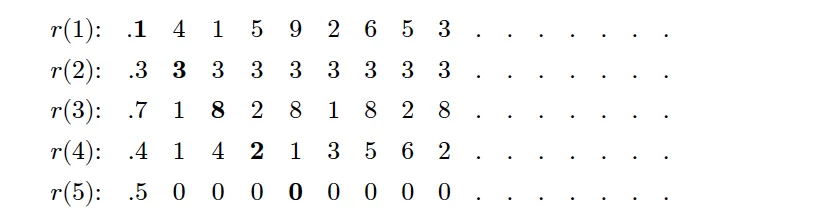
超级经典的 Cantor 对角线证明！

截图为敬！不可数（Uncountable) 集的诞生！

image.png

无穷大有好多种，我喜欢无穷大旅馆～

📎无穷大旅馆_数学爵士乐.pdf

（全书在这里 -> 📎数学爵士乐.pdf）


从 Bloop 到 Floop 到 Gloop

在我看来这一段就是计算机系学生的垂死挣扎。。。给一个没有解的数学问题做各种等价变化，试图让它有解，那怎！么！可！能！呢！

好吧去喝了一口水我忽然发现，这段的意义是：如果我们证不出来命题A，且我们不知道是不是某个大神在200年后就能证出来了，那么我们就假定也许命题A是能够证明出来的。在这个超级乐观宇宙里推演一下我们想要的超级美好结果是不是能够实现了！——然而这个想象被康托对角线无情地否定了 55555

所以这确实不是垂死挣扎，是小姑娘划亮最后一根火柴又看着它灭掉的悲伤故事。

忽然，人和机器，在“可计算性”上划了等号？

image.png

这个结论细思后忽然出现许多问号。它为计算机的能力划定了一个强硬的边界——计算机能算的，最多就是人也能算的。它比人强的地方，只是比人算得快一些。

而且算的还是 FLOOP。

人的思维是 FLOOP 吗？

如果是的话，计算机还有诞生思维的可能性？


一些相关文章

中文世界的对丘奇-图灵论题的讨论实在太少。

一篇不错的前因后果文：《丘奇－图灵论题（Church–Turing thesis） 》 by 悠扬的幻想天空 博客

上～梯～子～～

https://en.wikipedia.org/wiki/Church%E2%80%93Turing_thesis#The_thesis_as_a_definition

哲学暗示值得一个截屏！

image.png

https://mathworld.wolfram.com/Church-TuringThesis.html

短小精悍的介绍。全文截屏～

image.png




 

回到顶部