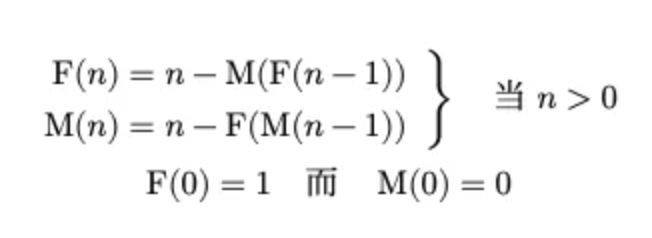C05 递归结构和递归过程
感觉分享会线上自己讲的,没我写的时候清楚,感觉表达能力还是欠缺。也可能是还不太习惯对着屏幕自言自语。总之分享会的录屏链接在这: 百度云盘 提取码: 78za
因为当时云记录好像地方不够了?我就录在了本地,其实不看也罢:P
见字如面
简介:
因为接了下一周(02.27号)的领读任务。所以准备在这里准备做个笔记/随时更新,回头「共读会」的会议笔记可能直接贴在文章的下面?或者再另起一篇(看情况)
因为是第2次读这一章/笔记可能会凌乱或者不全面,如有写的不对之处欢迎指正,留言补充。
PS:2022.02.26 我觉得这第五章讲的其实挺清楚的,而且每一部分都特别直给。好像没啥看不懂的?可拓展的背景知识也有点少。觉得自己写了这么多有点多余(画蛇添足)
「和声小迷宫」
作者用缩紧来表示进入不同的世界。
第1层
第2层
第3层
但每层都是 「乌龟」和「阿基」这2个人物的对话,可能「盗梦空间」的作者也看过这本书吧?
关于「灯神」的那一段,想到了Rick & Morty 里面的Mr Meeseeks,感觉那一集讨论的是同一个主题。
我们会发现在日常生活中对一个问题只要多问几次为什么?很多往往都能找到「递归」结构。而且神奇的是很多这样的问题,特别是主观的问题(比如如何学会的一件事情)我们并不知道它们是如何通过递归实现的
比如你是怎么样学会打球的?为什么这样就能学会呢?为什么这个方法能学会呢?为什么呢。。。
或者,你是怎么看见的?你能感知到你自己的视觉系统吗?
乌龟:堕界:没有打出来的嗝和已熄灭的灯光所在的地方。它是一种候室,在这儿处于休眠的软件等着宿主硬件回来。无法知道这个系统要瘫痪多久,我们会一直呆在堕界里,也许几分钟,也许要几小时、几天一-甚至几年。
想到了黑客帝国里,那个Neil永远逃不出去的火车站。我们生活中可能也有类似的结构?比如「重复无聊的生活」「某段情感纠葛」?或者「永远结束不了的读书会」
我猜「和声小迷宫」里面的2个角色,是作者听这首曲子时候的意识思维,而这个笔记是我的(我读这本书时候的意识思维) 所以整本书里的2个角色,可能都是作者在研究某个问题,为了研究明白时脑子里的意识思维。(即他当时的笔记) 就像我现在写了这些笔记,最终串起来一个导读稿一样,他用笔记弄了本书。(也算是递归了?)
名词对照:
Now we're in a pretty pickle, aren't we? 我们崴泥了,是吧?(没看懂这里面的隐喻)
Achilles: Oh, boy-popcorn! I'm going to munch my head off 阿基:哦,天哪 弹出锅酥!我可得甩开腮帮子足吃!
Tortoise: Let's just hope it isn't pushcorn! Pushcorn and popcorn are so extraordinarily difficult to tell apart. 乌龟(上一层的):可别是推入锅酥!推入锅酥和弹出锅酥可真不好分清呀。
Achilles: What's this about Pushkin? 阿基里斯:焚琴?你说什么呢?
(Pushkin好像是普希金的意思,这里是分清和焚琴的对应,因为话是上2层的乌龟说的,被这一层的阿基听到了)
Tortoise: I didn't say a thing. You must be hearing things. 乌龟:我什么也没说呀。你大概是有点⻛声鹤唳了吧。
Achilles: Go-golly! I hope not. Well, let's dig in! 阿基里斯:还煮鹤!我真的不喜欢鹤肉。好啦,我们就吃这个吧!
Tortoise:What an amusing story. Did you enjoy it? 乌龟:多有趣的故事啊。你喜欢它吗? (这里他们跳出了1层)
Achilles: Mildly. Only I wonder whether they ever got out of that Evil Majotaur's pit or not. Poor Achilles-he wanted to be full-sized again. 阿基里斯: 一般。我想知道的只是他们离开那邪恶大雕的窝没有。可怜的阿基里斯——他想恢复正常身高。(这里应该还暗指了他们的对话,现在是缩进格式的)
Tortoise: Don't worry-they're out, and he is full-sized again. That's what the "POP" was all about. 乌龟:别担心——他们出去了,他也恢复了正常身高。这就是刚才为什么有一声“弹”。
Achilles: Oh, I couldn't tell. Well, now I REALLY want to find that bottle of tonic. For some reason, my lips are burning. And nothing would taste better than a drink of popping-tonic. 阿基里斯:哦,我没听出来。嗯,我现在的确想找那瓶煮调饮了。不知为什么,我的嘴唇都要裂了。没有什么比弹出煮调饮更好喝的了。(弹出主调-饮)
Tortoise: That stuff is renowned for its thirst quenching powers. Why, in some places people very nearly go crazy over it. At the turn of the century in Vienna, the Schonberg food factory stopped making tonic, and started making cereal instead. You can't imagine the uproar that caused. 乌龟:这种饮料以消燥解渴著名。在有些地方,人们对它着了魔。在十九世纪末、二十世纪初的维也纳,勋伯格⻝品工厂停止生产煮调饮,转产十二瓶菌氯,你无法想象由此而引起的骚乱。(Schönberg food factory这里主要人物应该是Arnold Schönberg 他是第二维也纳乐派的核心人物,发明了十二音列作曲法,12平均律 企图取代传统的调性系统,无调性音乐(atonalmusic)等引起了当时不小的骚动)
Achilles: I have an inkling. But let's go look for the tonic. Hey-just a moment. Those lizards on the desk-do you see anything funny about them? 阿基里斯:我略有所闻。不过还是让我们找找那瓶煮调饮吧,嘿——等一会儿。桌上这些蜥蜴—— 你发现它们有什么特别的吗?
Tortoise: Umm ... not particularly. What do you see of such great interest? 乌龟:嗯——没什么特别的。你看⻅了什么这么有趣?
Achilles: Don't you see it? They're emerging from that flat picture without drinking any popping-tonic! How are they able to do that? 阿基里斯:你没看⻅?它们没喝什么弹出煮调饮就从那张平面上的画里跑出来了。它们怎么做到的?
Tortoise: Oh, didn't I tell you? You can get out of a picture by moving perpendicularly to its plane, if you have no popping-tonic. The little lizards have learned to climb UP when they want to get out of the two-dimensional sketchbook world. 乌龟:我没告诉你吗?要是你没有弹出煮调饮的话,你以同画面成直⻆的方向移动,也能从里面出来。这些小蜥蜴知道,要想从两维的画中世界里出来,就得向上爬。 (这里应该指的是12平均律,里面的技术关键点,你要想弹出主调,就需要升高一个调类似 C调-G调 ?我不是学音乐的,不太了解这部分,欢迎补充。但好像是类似听起来像永远在升高的音乐但其实是同一段的重复?)
。。。
有意思的是,他最终好像没有跳到最外层的那个世界,即就是去游乐场玩做「大风车」的那个 乌龟和阿基 所在的世界,而是结束在了他们读的那个故事里。
读完后也没有想明白最开始故事里的魔王/大风车作者是想指的是什么。日常生活的循环?大脑日常的循环体系?还是指的因果循环?
乌龟:我姑妈会算命,她对我说今天我会遇到好运。正是因为期待着那个好运我才这么兴奋的。
这部分表示的应该是语言对实际行为的影响?有些事儿你信了才是真的?
「递归迁移网络」
这部分,以及造物神的例子,应该是想说明「分形」(Fractal)我们日常使用的语言中也存在着这种分形结构(还有递归结构)我们平时说话传输的意义,其中有一部分是传输了这种结构。换句话说你有了跟作者一样的结构,才是理解了作者说的话,才知道这堆符号想表达的是什么(想到的例子:学英语还要学习文化/记笔记要画图)
从这个公式一直到Q函数这部分,作者应该是想介绍「复杂系统」里的一个基本概念即:
有序的方程式可以很轻易的制造出混乱
那人们很自然地会想到:表面上(人世间)的混乱是否隐含着某种微妙的规律性?
我找了几个线上的数学绘图工具/试图绘制这个F(n)/M(n)的函数,但没找到合适的工具绘制成功,连接可能原因是因为主要用到了递归?网页端的都不太好弄?也可能是因为我太菜了。
如果谁有Matlab或者其他什么合适的绘图工具/和开发环境欢迎告诉我哈。
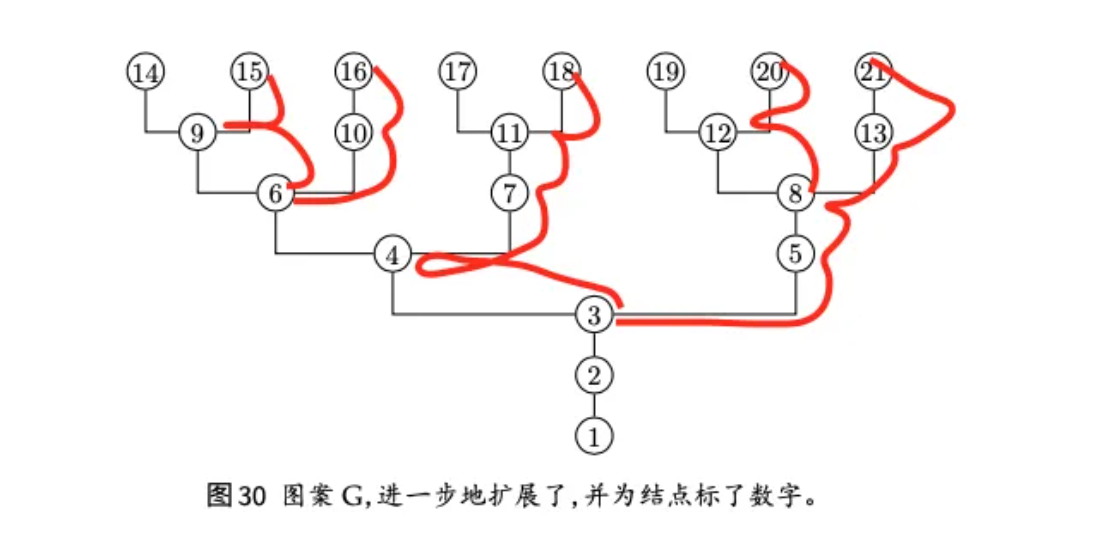
「图案G和递归序列」
这里应该是在展示数学中的某种「结构」这个结构有2个特性
1.这种结构和之前一章讲的语言/符号中的「结构」有同构性。
画红线的部分是图案/而没画线的部分是衬底。上一章的图案和衬底是在图画中,语言中,符号中,这里是在数学中,进一步也就是在人的思维中也存在着这样的图形和衬底。
2.这个结构是递归的,更确切的说,这个结构中图案的部分是递归的
这里的递归 or 分形 让我想到了电影「黑衣人」里的银河,那个不是银河的小副本,那个就是银河。或者说,那不是你的作品或者你的小副本,那就是你。
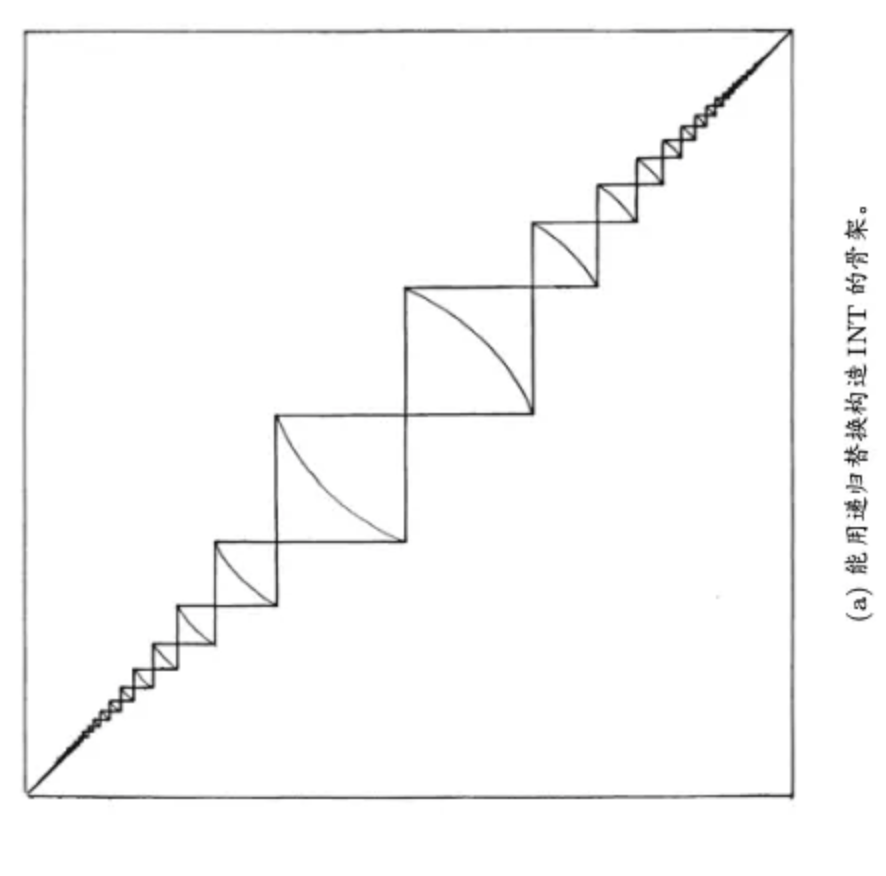
「两个令人惊异的递归图」
首先,对于⻣架的每个 方框,你要做两件事:(1) 把⻣架的一个弯曲了的小副本放进方框,用里面的弯曲的线作为它的向导;(2) 涂掉 外面的方框及其弯线。一旦把原⻣架的每一个方框都这样做了,每个大⻣架原来所在之处就换成了许多的“小 辈”⻣架。下一步,降一个层次对那些小辈⻣架重复这一过程。然后再重复,再重复,再重复......这样下去的极限 就是 INT 图,当然极限是达不到的。就这样,一层一层地把⻣架嵌套于它自身之中,INT 图就“无中生有”地逐 渐构造出来了。但事实上,这“无”不是虚无——是一幅图。
作者最想强调的,或者说最令人惊异的应该是这句话:我们看到了这个图形“无中生有”地逐渐构造出来了。但事实上,这“无”不是虚无——是一幅图。
「应无所住,而生其心」
我不该让读者到现在还不知道这些美丽图案的由来。INT——代表“交换”——是来自一个涉及了“埃塔序 列”的问题,与连分数有关。
。。。
G 图来自一个问题的高度理想化形式,这个问题是:“磁场中晶体的容许电子能是什么?”这是个很有趣的 问题,因为它交织了两个非常简单而又基本的物理现象:完全晶体中的电子,和均匀磁场中的电子。
这部分没太看懂,太过专业/但我看懂的部分是,作者在表明,这个数学中的「结构」和现实问题的关系也是同构的。即:人们将现实问题抽象成这个数学问题的过程是也是「结构」同构的
让我想到了薛定谔在「生命是什么」那本书中提出的观点,生命就是个「非周期性晶体」
没有磁场的晶体与没有晶体的磁场的确是有一个共同特征的:在两种情形中,电子都表现出周期性。于是,当两种情形合并在一起时,两个周期的比是个很关键的参数。事实上,这 个比率包含了有关容许电子能分布的全部信息——但是,只有展开成连分数时,它才透露它的这一秘密。
一种递归结构
我的一个持不可知论的朋友曾被 G 图的无穷多个无穷所震惊,于是把它叫做“上帝的画像”,我不认为这是 亵渎神圣。
想到了分形理论被称为「上帝的指纹」不知道作者在写书的时候,那篇论文有没有发表,如果没有,那写出上帝指纹的人一定也看过GEB
现在我们来换一种眼光,在这种眼光下,整个世界都是建立在递归之上的。
说的特别对,我们应该时刻保持觉观,去注意到生活中的递归,更有利于了解真实。
当相互作用的“开关”被“打开”时,粒子就像函数 F 和 M、或者说两个结了婚的人那样纠缠在一起。这些 实际的粒子称为“重正化了的”——一个丑陋但却有启发性的术语。结果是,一个粒子如果不涉及所有其它粒子 就无法给出定义,而其它粒子的定义反过来又要靠最初那个粒子,等等。这样转来转去,构成了一个永不停止的 循环。
刚结婚,对这段话特别有感触,那就是纠缠!可能量子怎么纠缠的夫妻就怎么纠缠!建议研究量子物理的,可以从不幸的夫妻生活中寻找灵感!丑陋但却有启发性,而且是永不停止的循环。
生命>离去>相爱>新生。。。这是一个循环是生命中的图案
吵架>不说话>交流>交流失败> 吵架 。。。是婚姻生活中的另一个循环,是生命中永恒的衬底 T_T
「费曼图」
费曼图我因为时间有限,背景知识不够,没看懂。特别是它底下的注视这句话:
时间从左向右增加,因此,在电子的箭头指向左边的片段 中,它的移动是“与时间反向的”。
直接给我干懵了。紧接着他的解释
更为直观的说法是,反电子(正电子)在正向的(即正常的)时间中移动。光子的反粒子是它们自己,因此它们的曲线无须箭头。
也没有很直观... 所以意思是光子不受时间影响?还有光子的反粒子为啥就是它自己了?(我感到自己背景知识不够理解这一部分的全部)
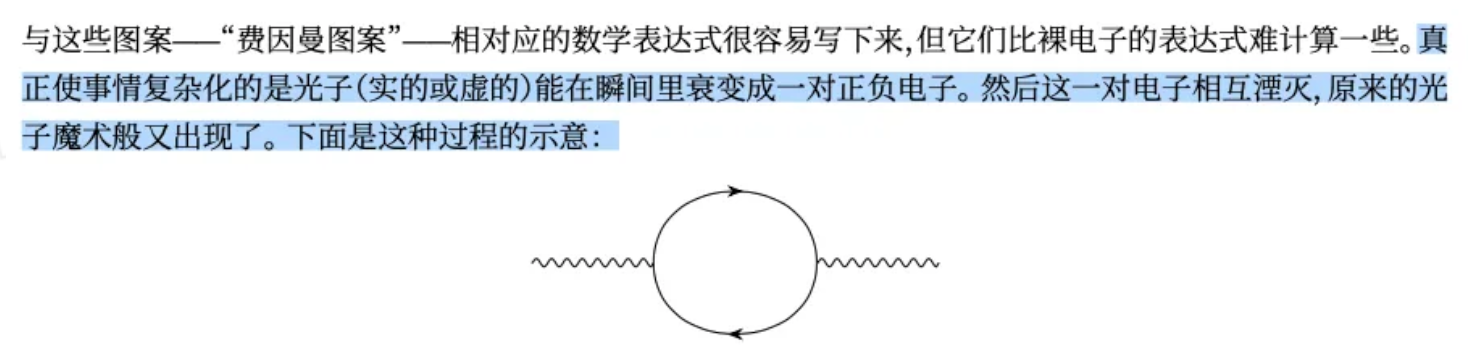
「使事情复杂化的是光子(实的或虚的)能在瞬间里衰变成一对正负电子。然后这一对电子相互湮灭,原来的光 子魔术般又出现了 」
读者或许已经预料到,这些虚的过程可以嵌套到任意深度。这可以产生出一些看起来非常复杂的图案
但整个部分的难点应该是我选中的这块儿,重要的光子衰变过程也是个「递归结构」
重整化(Renormalization)是量子场论、统计场论和自相似几何结构中解决计算过程中出现无穷大的一系列方法。(维基百科查到的)
但没看懂,但感觉它的应用场景是用数学工具来建模描述量子物理遇到的无穷大问题。
只要是粒子之间的相互作用,无论是什么类型的粒子,物理学家都用重正化的概念来理解所发生的现象。于是,质子、中子、中微子、π 介子和夸克——亚核子动物园中所有的动物——它 们在物理理论中都有裸的和重正化的形式。这些成千上万的泡泡套着的泡泡们就组成了这个光怪陆离的世界。
裸的是啥意思?没看懂。但这段儿整体是在说,整个世界从微观到宏观都有重正化结构。
「副本和同一性」
所有蝴蝶的“相同之处”是什么?一个蝴蝶到另一个蝴蝶的映射并非把细胞映射到细胞,而是把功能块映射 到功能块,其中,部分是宏观的,部分是微观的。映射所保持的不是功能块之间的精确比例,而是它们之间的功能关系。
想到了神经网络,也是用数学建模来表达关系。
什么时候两个东西是一样的?
这种探讨将在本书中一再出现。我们将从各个不同的⻆度来提出这个问题,最终,我们会看到,这个简单的问题 与智能的性质有着多么深刻的联系。
感觉点出了本书的核心。
「弈棋程序中的递归」
感觉作者是在说人类的智能活动都存在着「递归结构」的身影,并且还有一个重要的部分—— 跳出机制
有趣的是,我在写下这堆读书笔记的时候,并没有察觉到什么「递归结构」的出现,是不是说明我现在做的事情并不是智能的?还是在提醒我之后每次的读书都要站在作者的角度思考一下作者为啥要这么写?和他将会怎么写下去?以这样的方式引入博弈似的递归机制?
但是我确实察觉到了不少「跳出机制」可能是值得庆幸的地方:)
「递归与不可预期性」
感觉是在说不仅能「无中生有」而且可以产生不可预测性。而「设计出可以修改自身的程序」令人想到了反馈神经网络。以及冥想:应该就是在修改我们自身的程序。
读后感
我读完这章的主要联想是,我们好像确实不知道自己是怎么回事,不知道我们是怎么学会一个东西的?所有都是稀里糊涂就学会的,稀里糊涂顿悟的。比如我们怎么学会的骑车?打球和用筷子吃饭的?怎么学会的英语?中文?好像都是递归结构。
而我们本身又对清晰/明白这个过程有种执着,本能的执着,比如教育讲究确定性,国家讲究稳定。(就像图形和衬底)
而冥想应该是众多修改我们自身程序的方法之一。如果是这样的话,那么打坐或站觉观的时候一定要小心,如履薄冰。