C07 命题演算

本章节共读视频

链接: https://pan.baidu.com/s/1Yq7L-d4zn_0UiwC9BWOnoQ 提取码: ikga 

半音阶幻想曲 及互格

关于《半音阶幻想曲与赋格》：《半音阶幻想曲与赋格》BWV903是巴赫最著名的作品之一，然而也是最令人困惑的。尽管该作品对技巧和音乐的要求都极高。从18到19世纪仍然有三十多种手稿存在；其中有十几种至今下落不明，但是当时的销售和拍卖目录都记载了它们曾经存在过。

关于互格：互格？ 未解

阿基和乌龟的对话：

幻想规则里：<P →Q>，若P，则Q；

乌龟的问题：认可P，认可→，但不认可Q。 ——幻想规则的逆规则。 

看完后：为什么阿基到最后开始道歉？ 乌龟确定不是在PUA阿基？

问：标题与对话的关联性在哪里？

第七章-命题演算

词与符号、良构串

用符号来代替词。

∧——并且

∨——或者 （相容或）

【】——幻想规则中的推入和弹出符号

→ ——推导出的代指

～—— 非

～～——双非

各类规则

幻想规则（常被称作“演绎定理”）：

有那么一条规则，它无中生有地制造定理——它不需要一个“老定理”作为输入（其他的规则都是要求输入的）。

幻想规则示例：

【X ——幻想开始

.......

.......

.......

Y】——幻想结果

得到定理： <X→Y>

幻想规则可以递归，也就是幻想中可以套入幻想，如同嵌套的故事或者电影。此处联想到《楚门的世界》。

当你从一个电影中的电影里弹出来时，有那么一会儿你感到你好像已经到达了现实世界，但事实上你离开顶层还差一个层次。

幻想之中还有更多规则，汇总如下。

联结规则：如果x和y都是系统的定理，那么串<x∧y>也是该系统的定理。

分割规则：如果<x∧y>是一个定理，则x,y都是定理。

双重弯号规则：像“～～”这样的串可以从任何定理中删去。它也可以嵌入到任何定理之中，条件是所得的结果是良构串。

搬入规则：在一个幻想里边，任何来自于“现实性”高一个层次的定理都可以拿进并使用。

分离规则（Modus Ponens肯定前件式)：如果X和 <X→Y>二者都是定理，那么Y是一个定理。

易位规则：<X→Y>与<～Y→～X>是可互换的。

如果你正在学习“道”，那么你就远离了它。

如果你接近了“道”，那么你就不是在学习它。

德·摩根规则：<～x∧～y>与～<x∨y>是可互换的。

幡不在动，并且风也不在动。

或者幡在动或者风在动，这都不是真。

思维陀螺规则：<x∨y>与<～x→y>是可互换的。

要么一朵云正挂在山上，要么月光正在穿透湖水的波纹。

如果一朵云不挂在山上，那么月光正在穿透湖的水波。 ——这两者如何能够互换呢？

虽然很多句子看上去有点“胡说八道”，没有任何意义，但

这个系统——命题演算——是一步步很干净地从真走到真，仔细地回避所有的假。正像一个人一心要不弄湿脚，他就会在小河里小心地一步步从一块蹬石走到下一块，完全遵照蹬石的布局，而不管它可能是如何地曲来拐去和难走。

思考：法治与人治

半解释——若P，则Q。

禅宗公案——岩头之斧

中文原文：

“德山一日谓师（即岩头——译注）曰：“我这里有两僧入山，住庵多时，汝去看他怎生。”师遂将一斧去，见两人在庵内坐。师乃拈起斧曰：“道得也一下斧，道不得也一下斧。””

“二人殊不顾。师掷下斧曰：“作家！作家！”归，举似德山，山曰：“汝道他如何？”师曰：“洞山门下不道全无，若是德山门下，未梦见在。””

悟点：两个禅修的人没有理会，其实是跳出了“道得”与“道不得”的系统，得以存活。 当在一个系统中遇到矛盾时，跳出系统，去到系统之外。

英文原文：

One day Tokusan told his student Ganto, “I have two monks who have been here for many years. Go and examine them.” Ganto picked up an ax and went to the hut where the two monks were meditating. He raised the ax, saying “If you say a word, I will cut off your heads; and if you do not say a word, I will also cut off your heads.”

Both monks continued their meditation as if he had not spoken. Ganto dropped the ax and said, "You are true Zen students." He returned to Tokusan and related the incident. "I see your side well," Tokusan agreed, "but tell me, how is their side?" "Tõzan may admit them," replied Ganto, "but they should not be admitted under Tokusan."

文中使用了上述规则，共计24步推导出结论：两颗脑袋都要被砍掉。

命题演算给我们一组规则来产生语句，这些语句在任何可想象的世界中都是真的。这就是它的所有定理听起来如此简单的原因：它们似乎完全没有内容！从这种角度去看，命题演算可以看成是浪费时间，因为它告诉我们的东西完全是不足道的。从另一方面来说，它是通过详细说明那些普遍真的语句的形式来做这件事情的，而使得宇宙里核心的真理看得更清楚了：它们不仅是基本的，而且是有规律的：它们能用一组印符规则产生出来。

网友评论：

庵居坐禅本是洞山一系的门风，石霜有枯木众，后世倡默照禅，岂是虚然！德山令岩头评价二人，岩头言道，若是洞山门下，不能说全无可取，若是德山门下，则尚未梦见，差得很远。岩头不是说二人境界不及，而是怪他们投错了地方，若是洞山门下，定力深厚，堪称作家，而在德山门下，如此枯坐，驴年难悟！洞山门下有修有证，坐禅便是功夫；德山门下无修无证，宴坐即是执着。岩头并非有意贬低洞山，而是表明二宗门风不同。

德山禅宗：

德山宣鉴，俗姓周，二十岁出家，精通律藏，原来在四川讲 《金刚经》，后来前往江南挑战南禅，最终折服于南禅，由崇信(青岩系第四代禅师)接领顿悟，吹烛悟道。德山宣鉴以“禅风竢烈，大逆不道”而闻名，他的“说打三十棒，不说也打三十棒”的“德山棒”与“临济喝”齐名，他的“喝祖骂佛”更是影响大，争论多。天皇道悟这一法脉从他这里扬名，他的再传弟子后来开创了禅宗五宗中的云门宗、法眼宗。

<参考：作者：周脖通 链接：https://www.jianshu.com/p/5c6d77320f73>

洞山——曹洞宗

中国禅宗“五家“之一，属“青原“大系。创始人为唐代良价禅师（807-869）和本寂禅师（840-901）师徒二人。因良价住江西宜丰的洞山，本寂住江西抚州宜黄县的曹山，故称“曹洞宗“。该宗门风不象临济宗那样峻烈，而似精耕细作的老农，温和细密，言行相应，随机应物，就语接人。其门庭设施为五位之说，分为偏正五位和功勋五位，各以君臣、父子关系说之。每一对都以互相配合而构成五种形式，其中以偏正五位为基础，辨明体用，扫荡情尘，使其物我双忘，人法俱泯。在禅宗五家之中，其门叶虽不及临济宗之繁盛，但法脉绵延不断，直至当今。江西云居山真如禅寺、湖北汉阳归元寺都是曹洞宗寺院。

系统是一致的吗？

如果我们用规则同时推导出了X和～X ， 两者都是定理吗？那么系统是一致的吗？

是否有一个证明，能够证明所有定理都为真？ 或者X和～X 不会同时是定理。

你无法永远维护你的推理模式。

捷径与导出规则

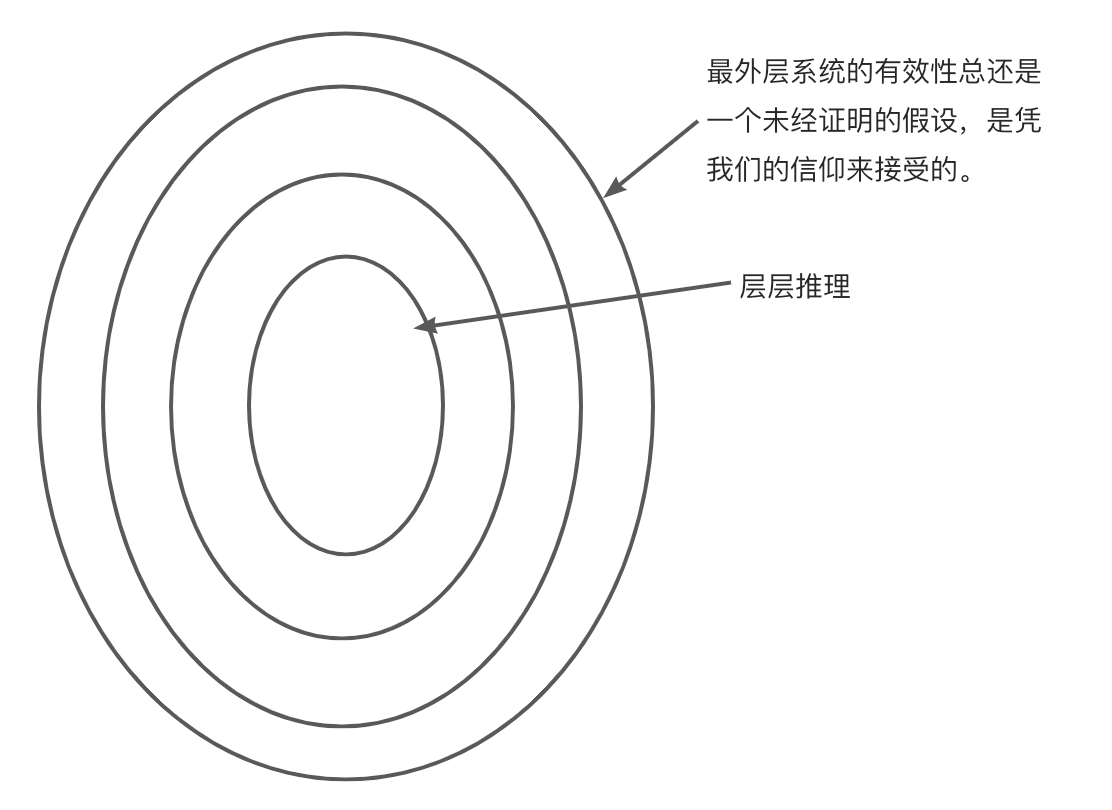
蛋的最外层是： 元理论，元理论导出元定理，元定理是有关定理（可导出的串）的定理（被证明了的结果）。

导出规则 与 规则的区别

从<P∨～P> 到<Q∨～Q>， 采用定理图式，可以高效地被利用，也就是“捷径”。 但，导出的规则并不是命题演算的“规则”，因为不能保证 导出的规则 始终是一个定理。

承认导出规则是命题演算中的一部分，就丢掉了系统的形式性，因为导出规则是非形式地导出的，是在系统之外的。

那么是否可以将元理论形式化？但总有元理论之外的元元理论，关于系统的思考就将成为系统里的一种工作方式——引出，系统是否能够“对自身进行思考”？

如果你没有仔细地将在系统里的工作（J方式）与对于系统的思考（W方式）区分开，就会产生出谬误来。

证明和推导

命题演算非常像以某些方式进行的推理，但是人们是不应该把它的规则与人的思维的规则同等看待的。

任何一种简单性都会带来一种特殊类型的复杂性。对于证明，是他们赖以依靠的背景系统——即，人的语言——的复杂性；对于推导来说，这是它们的天文规模，这使得它们几乎是不可能把握得住的。

以前述乌龟和阿基的例子为例，用语言，简单的事情复杂化，并且并没有能够说服乌龟。

关于矛盾

书中从<P∧～P>推导出了Q，得到一个古怪的解释：P和非P合在一起蕴含Q。

从一个矛盾出发，结果可以是任何东西！

——以命题演算为基础的系统中，不能包含矛盾。

人的思维是可以处理矛盾，包括在数学领域，对于矛盾的发现和修正是加强而不是削弱了数学。

现实矛盾：我们真正进行思考的方式与命题演算模仿我们的方式二者之间的矛盾。

人：带有不一致性的推理；

命题演算：带有一致性的证明。

衍生推荐

希瑞推荐：《绝美之城》

小章鱼推荐：公众号-他者others

曹原推荐：书籍

《适者降临》

《复杂生命的起源》